Newtons gravitations- och rörelselagar

Grunden i mitt program för att beräkna planeternas banor är Isaac Newtons gravitationslag och rörelselagar. Albert Einstein visade i sin Allmänna relativitetsteori att Newtons lag bara är en approximation, men en mycket god sådan i omgivningar med låga hastigheter och gravitationsfält, som i solsystemet. Hastighet i det här sammanhanget är hastighet i förhållande till ljushastigheten… Även om de relativistiska effekterna inte är helt försumbara, har jag av valt att i mitt program utgå från den klassiska Newtonska världsbilden och sedan göra korrigeringar för de relativistiska effekterna.

Newtons gravitationslag säger att två massor, M och m, dras mot varandra med kraften F enligt:

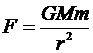[1]

Där G är gravitationskonstanten (ca 6,6742×10^-11 Nm²/kg²) och r är avståndet mellan massorna masscentrum. Newtons andra rörelselag säger att om massan m accelereras med acceleration a går det åt kraften F enligt:

[2] (fet stil i ekvationerna betecknar att symbolen är en vektor)

Använder man Newtons tredje rörelselag, som säger att en kraft alltid åtföljs av en lika stor och motriktad kraft, och sätter [1] lika med [2] får man för två himlakroppar den acceleration tyngdkraften från den ena accelererar den andra när de dras mot varandra:

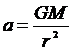för M:s påverkan på m, samt för m:s påverkan på M [3]

Storleken på tyngdkraftsaccelerationen är alltså inte beroende på massan av det föremål som påverkas. Det enda som har betydelse är den påverkande massan och avståndet från denna.

Om vi går vidare med rörelselagarna och ser på sambanden mellan position, hastighet och acceleration har vi följande formler:

[4][5][6]

Där r är position, v hastighet och a acceleration efter tiden t. Eller rättare sagt [4] och [5] talar om förändring av position och [6] förändring av hastighet. Om föremålet eller himlakroppen, som är det vi håller på med, redan har en känd position och hastighet vid en viss tidpunkt kan vi använda [4] och [6] för att få fram en ny position och hastighet för himlakroppen Δt tid senare.

[7][8]

Där r₀ och v₀ är position och hastighet vid tiden t₀, r₁ och v₁ position och hastighet vid tiden t₀+ Δt, v och a den konstanta hastigheten och tyngdkraftsaccelerationen under perioden Δt.

Det är väldigt vanligt att man använder begreppet derivata för att beskriva sambandet mellan r, v och a. v är då tidsderivatan av a, r tidsderivatan av v. r är också andraderivatan av a:

eller med annan notation: [9][10][11]

Nåja, det verkar ju rätt enkelt att räkna ut positionen för en planet. Man räknar ut tyngdkraftsaccelerationen enligt [3] och använder den för att räkna ut hastighet och position enligt [7] och [8], men riktigt så enkelt är det inte. Det som ställer till det är att storleken och riktningen av a och v aldrig är konstant. Detta innebär att det faktiskt är omöjligt att i teorin exakt beräkna himlakropparnas banor i solsystemet.

Som vi ser ovan påverkas a av r, r av v och v av a. Om vi antar att vi räknar ut a₀ för månen vid tiden t₀för att sedan räkna ut r₁ och v₁ vid tiden t_1. Mellan t₀ och t₁ så förflyttar sig ju månen, vilket innebär att a antar olika värden under denna period (a beror på r). Detta innebär i sin tur att v₁ och r₁ blir fel eftersom de beräknades från a₀ som inte är ett korrekt värde på a under perioden. Det vi istället behöver är a och v:s genomsnittliga värde mellan t₀ och t₁. Det är metoder för att få fram dessa genomsnittsvärden avsnittet integrationsmetoder handlar om.

När man rent praktiskt räknar med vektorerna a, v och r får man dela upp dem i dess komponenter i x-, y- och z-led, så att r delas upp i (r_x, r_y, r_z) eller enbart (x, y, z), detta är alltså himlakroppens koordinater i det koordinatsystem man använder vid beräkningen. På samma sätt kan v delas upp i (v_x, v_y, v_z) och a i (a_x, a_y, a_z), som alltså är himlakroppens hastighet i x-, y-, och z-led samt den acceleration som gravitationen påverkar himlakroppen med i x-, y- och z-led. I alla vektorberäkningar är Pythagoras sats mycket användbar, med den räknar man ut längden av vektorn utifrån dess koordinater:

[12] r (utan fetstil) eller |r| är alltså längden av vektorn r.

Detta är alltså avståndet från origo i koordinatsystemet till himlakroppen. För att räkna ut avståndet mellan två himlakroppar får man använda [12] på differansen av deras koordinater:

[13]

För tyngdkraften behöver man gå åt andra hållet också. Man vet storleken på a enligt [3] men behöver dela upp den i dess x, y och z komponenter. För en sfärisk himlakropp kan man räkna på tyngdkraften som om hela kraften kommer från en enda punkt, nämligen himlakroppens centrum. Och centrum är också den punkt vi använder för att ange himlakroppens position. Så riktningen på a blir r, fast i motsatt riktning (sett från jorden är riktningen till månen utåt från jordens centrum, medan jordens tyngdkraftspåverkan på månen är åt samma håll men inåt mot jordens centrum), vars x-, y- och z-andel (enhetsvektor) är (-x/r, -y/r, -z/r). Ekvation [3] kan då skrivas om på följande sätt:

[14]