Korrigering för himlakropparnas form

I avsnittet om Newtons tyngdkraftslag behandlar vi himlakropparna som punktmassor, dvs. som om hela deras massa finns i en punkt i centrum. Detta går bra förutsatt att himlakroppen är en perfekt sfär. Nu har de flesta himlakroppar mer eller mindre avvikelser från den sfäriska formen och det är hur dessa avviklser påverkar tyngdkraften vi ska beräkna här.

Det mesta av informationen i det här avsnittet har jag hämtat från 70 x 70 Earth Gravity Model

Om vi ser till jorden har jordklotet en märkbar utbuktning runt ekvatorn som fungerar som ett handtag för tyngdkraften att dra i. Jordens ekvatorradie är 6378 km medan polradien är 6357 km. Det är dragningskraften från i första hand solen och månen på denna utbukning som orsakar jordaxelns precession. Månen är inte lika tillplattad runt polerna som jorden men har istället en obalans så att den sida som är riktad mot jorden har en högre massa, vilket har gett jorden ett handtag att dra i så att månens rotationstid med tiden blivit lika med hennes omloppstid.

För att beräkna effekten av dessa avvikelser använder man ekvationer som kallas Spherical harmonics. Det vi kommer att göra är att först beräkna gravitationspotentialen och sedan ta gradienten (derivatan) av denna för att få fram tyngdkraften. Ekvationen för den totala sfäriska gravitationspotentialen U för en himlakropp uttryckt i sfäriska koordinater är:

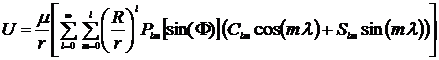[1]

Där μ är himlakroppens massa gånger G; R är ekvatorradien; r, Φ, λ är koordinaterna för den punkt vi vill beräkna U i, r är avståndet, Φ är latituden och λ är longituden uttryckt i himlakroppens lokala koordinatsystem; C_lm och S_lm är konstanter som beskriver himlakroppens form; P_lm[sin(Φ)] är ett s.k. associerat Legendre-polynom; l och m är den geopontentiala ordningen och graden, ju högre dessa koefficienter är ju finmaskigare bestäms klotytans form.

Spherical harmonics är uppdelade i tre underavdelningar, zonal harminics, sectorial harmonics och tesseral harmonics.

Zonal harmonics har m=0 och är band i latitudled på klotytan, antalet band är l+1. Som nämnts ovan är ekvatorbulan den största avvikelsen från jordens sfäriska form och den anges med koefficienten C₂₀. Här är l=2, vilket delar upp jorden i tre band där det mittersta är ekvatorregionen. En vanlig benämning på koefficienten C_lm är J_l med sambandet J_l= -C_lm (J₂ = -C₂₀)

Sectorial harmonics har l=m och är sektorer i longitudled, tänk apelsinklyftor, av olika bredd. Antalet är 2 gånger l. För månen är koefficienterna C22 och S22 viktiga och beskriver månytans form uppdelad i fyra klyftor.

Tesseral harmonics har 0 < m < l och delar in ytan i ett rutmönster.

Legendre-polynomen i ekvationen ovan har dessa utseenden för de lägre värdena av l och m:

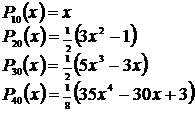
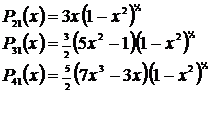
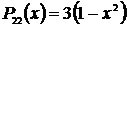
I vårt fall är alltid x=sin(Φ) i Legendre-polynomem.

Genom att göra ett koordinatsystem med origo i himlakroppens centrum blir koefficienterna C₁₀, C₁₁ och S₁₁ alla 0. C₀₀ blir potentialen för den sfäriska formen. Om vi bara tar med skillnaden i gravitationspotentialen jämfört med en perfekt sfär kan [1] skrivas om enligt:

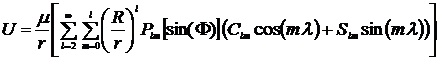[2]

Vi behöver också formler för att räkna om mellan sfäriska koordinater och kartesiska:

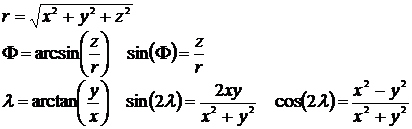[3] [4] [5]

Nästa steg är att räkna ut tyngdkraftsacceleration som man får genom att ta gradienten av U, enligt:

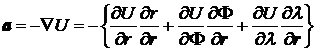[6]

Uppdelat i x, y och z-komponenterna kan [6] skrivas om enligt:

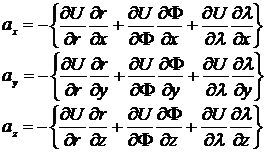
[7] [8] [9]

Termerna ∂r/∂r, ∂Φ/∂r och ∂λ/∂r är konstanta uttryck och ej beroende av U. Dessa termer är alltså derivatan av r, Φ och λ avseende på r som är positionen för den punkt a ska beräknas (t.ex kan r vara månens x, y, z-koordinater uttryckt i geocentriska koordinater). Uträknat blir de följande:

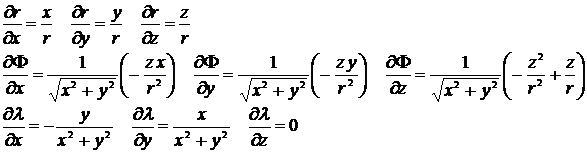[7] [8] [9]

Härledningen av dessa derivator tar jag inte upp här, men med hjälp av gymnasieskolans formelsamling och en lärobok i matematik lyckades jag göra härledningen. Man kan ju också göra numeriska stickprov och t.ex beräkna ΔΦ/Δx för olika x, y och z, med ett litet Δx och Φ enligt formel [3].

Den generella formen för derivatorna ∂U/∂r, ∂U/∂ Φ och ∂U/∂ λ är:

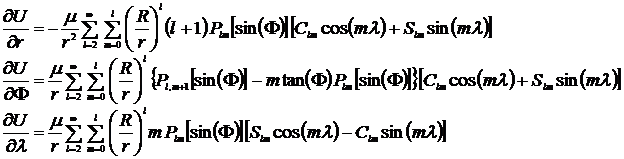[10] [11] [12]

Transformering av koordinater

Innan vi kan börja att använda alla de här formlerna måste vi se till att våra koordinater är uttryckta i rätt koordinatsystem. Formlerna ovan förutsätter att vi har alla koordinater i ett koordinatsystem där origo är i himlakroppens centrum, z-axeln är himlakroppens rotationsaxel, xy-planet är genom ekvatorn och x-axeln är riktad enligt himlakroppens lokala koordinatsystems noll-longitud. I mitt program använder jag normalt heliocentriska ekliptikala koordinater, därför måste koordinaterna transformeras till det lokala koordinatsystemet innan korektionen beräknas. Korrektionens x-, y- och z-delar måste sedan transformeras tillbaks till det ursprungliga koordinatsystemet innan de adderas.

Med hjälp av dessa generella formler följer nu uträknade exempel för fallen l=2 m=0 (J₂), l=3 m=0 (J₃), l=4 m=0 (J₄), l=2 m=2 (C₂₂ S₂₂).

Korrektion för J₂-faktorn

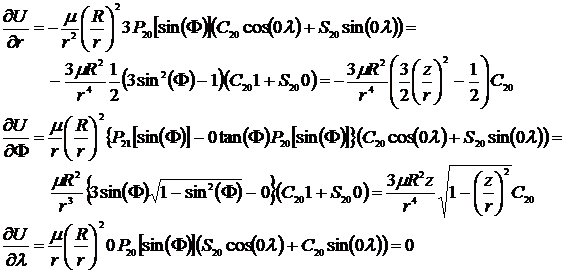[13] [14] [15]

Vi kan se att ∂U/∂λ blir 0, vilket är logiskt om man tänker på att här beräknar vi korrektion för en symetrisk utbuktning runt ekvatorn i ett koordinatsystem där xy-planet är ligger i ekvatorplanet. Formen är då symetrisk i longitud-led och vi behöver bara beakta avståndet och latituden. Genom att kombinera [13], [14] och [15] med [7], [8] och [9] får vi:

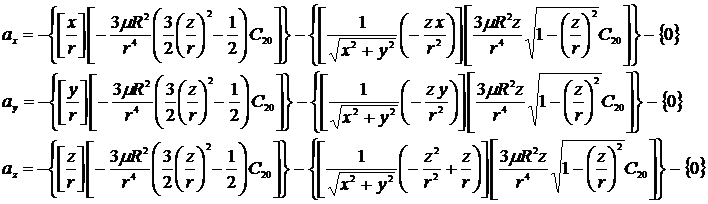[16] [17] [18]

Om vi räknar ut hur månen störs av jordens ekvatorbula är a_x, a_y och a_z korrigeringen av tyngdkraftsaccelerationen orsakad av jorden på månen i x-, y-, och z-led; μ är jordens massa gånger gravitationskonstanten; R är jordens ekvatorradie; r är avståndet mellan jordens och månens centrum; x, y och z är månens geocentriska ekvatoriella koordinater; C₂₀ är en konstant, för jordens del lika med 0,001082626.

Eftersom det till varje kraft finns en lika stor och motriktad kraft påverkas också jorden av månen. Påverkan på jorden får man genom att byta ut jordens μ mot månens och multiplicera resultatet med -1 i ekvationerna [16], [17] och [18]. Lättast är att bryta ut μ ur ekvationerna och multiplicera med μ_j och –μ_m i efterhand.

Man får inte heller glömma att transformera tillbaks resultatet till rätt koordinatsystem.

Korrektion för J₃-faktorn

J₃ är korrektionen för himlakroppens ”päronform”. Beräkningen är snarlik den för J₂ och korrektionsformlerna för tyngdkraftsaccelerationen blir:

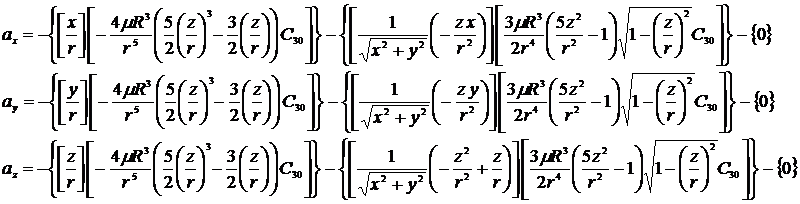
[19] [20] [21]

Korrektion för J₄-faktorn

J₄ är korrektionen för himlakroppens in- och utbuktningar i området mellan ekvatorn och polen. Korrektionsformlerna för tyngdkraftsaccelerationen blir:

[22] [23] [24]

Korrektion för C₂₂/S₂₂

I fallet med l=2 och m=2, himlakroppens ”apelsinklyftsform”, kommer även longituden med i bilden. I fallet hur jorden påverkas av månen måste månens librationsvinklar beräknas. Jag redovisar här bara formlerna för ∂U/∂r, ∂U/∂Φ och ∂U/∂λ.

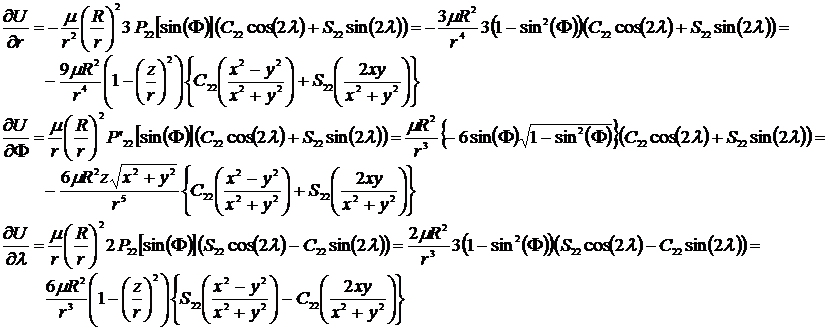
[25] [26] [27]